INTRODUCCIÓN

 

El presente blog tiene como objetivo, comprender la importancia del estudio del concepto y el Juicio. Un concepto es una abstracción de un conjunto de objetos, propiedades o eventos existentes en el mundo real o un mundo posible, que puede poseer una realización física en una lengua natural o sistema de representación determinados, al cual se puede hacer referencia mediante un símbolo arbitrario, aunque necesariamente único, dentro de un sistema representacional. Como constructo, posee ciertas propiedades distintivas de los demás conceptos, con los que guarda diversos tipos de relaciones. Tanto sus propiedades intrínsecas como sus relaciones con los demás conceptos deben ser evidentes, y por tanto susceptibles de ser especificados de forma explícita.

Explicaremos lo que se puede llegar a entender como juicio para así poder saber cuáles son los elementos y los tipos de juicios que existen, primero debemos saber que el juicio es la estructura lógica fundamental que nos pueden servir para así llegar a formar un juicio afirmativo. Se explica los factores que pueden llegar a intervenir por cada persona siendo ya en forma positiva o negativa, pero no siempre estos factores intervienen en forma espontánea por la persona, para saber cuáles son esos factores pueden llegar a conocerlo en este trabajo y así podrán aclara las dudas que se lleguen a tener sobre este tema o llenar algunas lagunas si la tienen. También se explica lo que corresponde para poder crear un juicio se necesita el conocimiento, la razón, el raciocinio como otros explicados a continuación.

APRENDAMOS DE LOGICA

 

1. EL CONCEPTO COMO REFLEJO DE LO UNIVERSAL DE LOS FENÓMENOS

El Concepto

El concepto es una forma del raciocinio humano, mediante la cual se expresan los caracteres generales de las cosas. El proceso del conocimiento de la Naturaleza por el hombre comienza con las percepciones sensoriales, por la observación directa de tales o cuales cosas y fenómenos de la Naturaleza. Pero el conocimiento no queda detenido en esta primera fase; se eleva a la fase superior, a la de la formación de conceptos, de categorías y de leyes. El concepto es el resultado de la síntesis de la masa de fenómenos singulares. En el proceso de esta síntesis abstraemos las propiedades y momentos casuales y no esenciales de los fenómenos, y formamos conceptos que reflejan las conexiones y las propiedades esenciales, fundamentales, decisivas, de los fenómenos y de las cosas. En el proceso de la formulación de los conceptos se crea el peligro de su alejamiento de la realidad. Por ejemplo, el concepto de número nació mediante la abstracción de los números singulares, particulares, que señalan tal o cual cantidad de cosas concretas. Sin embargo, los idealistas siguen considerando hasta hoy que el concepto de número, como los demás conceptos matemáticos, son apriorísticos, que existen antes e independientemente de toda experiencia del hombre. La lógica formal, idealista, enseña, que el concepto, como lo general, está completamente abstraído de todo lo particular y concreto. La dialéctica materialista denuncia el carácter metafísico de semejante separación entre lo general y lo particular y concreto. El materialismo dialéctico parte del criterio de que las síntesis auténticamente científicas de la realidad realizadas en los conceptos, llevan implícita toda la riqueza de lo particular, de lo individual, de lo singular. Los conceptos científicos comprobados por la práctica, son una verdad objetiva, dan un reflejo profundo de la realidad. En los Cuadernos Filosóficos Lenin define de esta manera el papel que los conceptos científicos desempeñan en el conocimiento: “El raciocinio, elevándose de lo concreto a lo abstracto, no se aleja, si es un raciocinio justo... de la verdad, sino que se acerca a ella. La abstracción de materia, de ley de la Naturaleza; la abstracción de valor, &c.; en una palabra, todas las abstracciones científicas (justas, serias, no absurdas) reflejan más exactamente, más profundamente, más plenamente la Naturaleza. De la observación viva al raciocinio abstracto, y de él a la práctica, tal es la senda dialéctica del conocimiento de la verdad, del conocimiento de la realidad objetiva” (Lenin).

Extensión y comprensión de los conceptos.

La comprensión es el contenido del concepto, es decir, el conjunto de notas esenciales o elementos de que consta un concepto. Así la comprensión del concepto hombre implica las notas esenciales o elementos siguientes: ser, viviente, racional, social, etc.

La comprensión o contenido de un concepto puede aumentar o disminuir; podemos agregar notas o elementos del objeto antes ignoradas, o restarle referencias a notas que las considerábamos y luego hallamos que no existen.

La extensión se refiere al número de objetos que caen dentro del concepto. Es la clase formada por todos los individuos, objetos o sucesos a los cuales puede aplicarse el concepto.

El término es la expresión de un concepto. Son términos únicamente las palabras, frases o signos que realmente expresen conceptos, de lo contrario, las palabras no pasan de ser sonidos o combinaciones de sonidos. Para que el término sea tal, necesita expresar la comprensión y la extensión del concepto.

Un concepto puede ser expresado por una o varias palabras; por ejemplo: “Ecuador”, “América latina”, “el área de la producción industrial”.

A veces un mismo concepto puede ser expresado por dos o más palabras distintas que reciben el nombre de sinónimas (de igual significación), por ejemplo: “idioma”, “lengua”, “habla”.

Cuando las mismas palabras sirven para expresar distintos conceptos se llaman homónimas (de igual nombre); por ejemplo “casa” (habitación) y “casa” (del verbo casar). Estas palabras se denominan términos equívocos, porque pueden conducir a error si no se especifica su sentido.

División de los términos.

Propiedades de los conceptos: extensión y comprensión. Ley de variación inversa

Los conceptos se emplean para nombrar objetos, ya sean reales o irreales, concretos o abstractos, mediante un conjunto de características distintivas. En este sentido cabe distinguir dos propiedades de los conceptos: la extensión y la comprensión. Los objetos referidos por los conceptos constituyen su extensión. En cambio, la comprensión de un concepto consiste en el conjunto de características distintivas de la clase de objetos.

Clasificación de los conceptos

Los conceptos se pueden clasificar de acuerdo con su extensión, su comprensión y su relación recíproca.

De acuerdo con la extensión, encontramos tres clases:

1. Universales. Refieren a todos los individuos de una clase o conjunto de objetos. Ejemplo: todos los mexicanos, ningún guajolote, el ser humano, las ballenas, las leyes,

2. Particulares. Refieren a un segmento de una clase o conjunto de objetos. Ejemplo: algunos mexicanos, la mayoría de los migrantes, pocos aspirantes, varias personas, muchos peces.

3. Singulares. Refieren a un solo individuo. Ejemplo: el autor de Cien años de soledad, Mario Vargas Llosa, Don Quijote, Marte, la Luna. 

De acuerdo con su comprensión, podemos identificar cuatro clases:

1. Simples. Contienen una sola característica y se expresan a través de un término. Ejemplo: libro, autor, mexicano, fama, internacional, Juan Rulfo.

2. Complejos. Contienen diversas características y se expresan a través de dos o más términos. Ejemplo: el autor del libro, el mexicano de fama internacional, el autor mexicano del libro de fama internacional.

3. Concretos. Expresan una cualidad haciendo referencia al sujeto que la posee. Ejemplo: niño pobre, maestra amable, hombre necio, mujer delgada, bebida amarga.

4. Abstractos. Expresan una cualidad sin hacer referencia a sujeto alguno. Ejemplo: pobreza, necedad amabilidad, delgadez, amargura.

5. Unívocos. Tienen una sola acepción o sentido. Ejemplo: agua, lápiz, ciudad, piraña, humano, jabón, edificio, envidia, monarca.

6. Equívocos. Tienen diferentes sentidos. Ejemplos: mariposa, papel, hombre, taza, nube, vestido, tenis.   

De acuerdo con su relación recíproca existen:

1. Subordinados. Cuando la extensión de un concepto es contenida dentro de la extensión de otro. El concepto de mayor extensión se llama subordinante y el de menor extensión subordinado. Ejemplo: polígono-triángulo, funcionario público-legislador, legislador-diputado, animal-perro.

2. Coordinados. Cuando los conceptos son subgrupos de un mismo conjunto. Ejemplo: perro-gato, avión-barco, bar-restaurante, refrigerador-lavadora.

3. Independientes. Cuando los conceptos no guardan ninguna relación entre sí. Ejemplo: limón-China, negro-virus, lente-hamburguesa.

1.2 La Definición

Definición significa acción y efecto de definir. Definir es fijar con claridad, exactitud y precisión, el significado de una palabra, la naturaleza de una persona o una cosa, o decidir o determinar la solución de algún asunto o cuestión. Etimológicamente, la palabra proviene del latín definitĭo, definitiōnis.

Así, una definición es la proposición o fórmula por medio de la cual se expone, de manera clara y exacta, los aspectos genéricos y distintivos de alguna cosa, bien sea material, bien inmaterial, para diferenciarla del resto. En el plano lingüístico, por su parte, la definición es el enunciado breve en el cual se expone de manera clara y precisa la significación de un vocablo, una locución o una frase. Este tipo de definiciones son típicas de los diccionarios, los vocabularios y los glosarios. Definición también se llama la decisión o determinación tomada por una autoridad legítima en relación con una duda, un pleito o una disputa. Asimismo, definición también puede hacer referencia a la nitidez de una imagen, es decir, al elevado nivel de detalle y calidad que tiene una imagen reproducida por un televisor, una cámara fotográfica o un proyector cinematográfico.

En este cuadro se muestran los distintos tipos de definición que, a su vez, son maneras distintas de definir. Una primera división distingue las definiciones en reales y nominales. Una definición es real si su definición es un concepto, cuya esencia ha de precisarse.

«Un triángulo es una figura plana y cerrada, formada por tres líneas que se cortan dos a dos».

Se dice «real» porque quiere referirse a la esencia de la cosa tal como es y, en su deficiencia (no se definen cosas), al concepto que ocupa el lugar de la cosa. Una definición es nominal si se define el uso de un término.

¿Qué son las Operaciones conceptuadoras?

Constituyen un aspecto necesario y fundamental del quehacer científico, en la medida en que toda ciencia, en un momento dado, requiere delimitar definir o precisar sus objetos de investigación, así como clasificarlos y dividirlos cuantas veces sea pertinente.

Por ejemplo: Se utilizan en la vida cotidiana, en nuestras reflexiones, conversaciones, argumentaciones etc.

Tipos de definición

Definición por Género próximo y diferencia específica:

Es la definición tradicional postulada por Aristóteles como ejemplar. Consiste, precisamente en la caracterización de un objeto o ser, por la investigación de su género próximo y su diferencia específica son las características que lo distingue.

Por ejemplo: “El triángulo es un polígono que consta de tres lados”

Definición nominal o etimológica: Consiste en recurrir a las raíces etimológicas de la palabra que designa al objeto que se va a caracterizar.

Por ejemplo: “Filosofía”, según sus raíces: philos, “amor o amistad”, y Sophia, “sabiduría”.

Definición genética: Se caracteriza al objeto señalando su origen o proceso de formación.

Por ejemplo: “La esfera es un cuerpo generado por un semicírculo que gira sobre su diámetro”

• La definición no debe ser demasiado amplia.
• La definición, no debe ser demasiada restringida o estrecha.
• Lo definido no debe entrar o estar incluido en la definición.
• Evitar círculos viciosos.
• La definición no debe ser negativa.
• La definición debe ser sencilla y clara.
• Es el análisis o descomposición de una totalidad en sus partes esenciales.
• Trata de llegar a elementos tan simples que ya no sean susceptibles de descomponerse.
• En una división todas las partes deben ser consideradas.
• En una división una de las partes no debe estar incluida en otra.
• Las partes de la división obtenida tienen que ser de la misma especie.
• La división tiene que seguir un orden dado por el objeto.

Se denomina clasificación, y consiste en ordenar en forma metódica, diferentes conceptos subordinados que se derivan de un supraordenado.

·         El concepto por clasificar. 

Por ejemplo: El triángulo.

·     El criterio clasificador o punto de vista que adoptamos en una clasificación.

Por ejemplo: Clasificar al triángulo desde el punto de vista de su angularidad.

·         Los miembros de la clasificación.

Por ejemplo: La clasificación de triángulos en

Acutángulos, Obtusángulos y Rectángulos.

·      Los miembros de la clasificación deben obtenerse de acuerdo con un mismo criterio clasificador.

·         La clasificación ha de ser completa y exhaustiva.

·         En la clasificación un miembro no debe estar incluido en otro.

·         La clasificación debe seguir un orden lógico

Tipos de Errores

Los errores de longitud son diferencias entre el valor verdadero del objeto y el valor medido, o entre el valor de referencia y el valor medido. Se expresan como "error = valor medido - valor verdadero". En realidad, es difícil obtener el valor verdadero sin importar cuán precisa sea la medición, por lo que es inevitable que exista cierta incertidumbre en el valor medido.

Los errores se pueden clasificar en tres tipos principales, en función del factor que genera el error. Tales factores deben ser considerados cuidadosamente para prevenir errores.

(1) Errores sistémicos

En este tipo de error, el valor medido está sesgado debido a una causa específica. Los ejemplos incluyen variaciones de medición resultantes de diferencias entre instrumentos individuales (errores instrumentales), temperatura y maneras específicas de medición.

(2) Errores aleatorios

Este tipo de error es causado por circunstancias aleatorias durante el proceso de medición.

(3) Errores de negligencia

Este tipo de error es causado por la inexperiencia u operaciones incorrectas realizadas por el personal que realiza la medición.

1.3 Definición del Concepto de Forma Lógica

Una forma lógica es una estructura ordenada constituida por partes y sus relaciones. Esta estructura ordenada subyace a nuestras proposiciones del lenguaje natural y nos señala algunas propiedades lógicas de tales proposiciones, Cuáles son las operaciones lógicas que incluyen tales proposiciones. Las partes de una forma lógica son variables proposicionales del tipo {p,q,r,s,t}  y conectivos u operadores lógicos incluidos en la siguiente serie: {―, &, v, →, ↔}.

Así la forma lógica puede verse desde dos puntos de vista:

Como la estructura ordenada subyacente a cualquier proposición del lenguaje natural, indicando sus propiedades lógicas, o bien, Como el resultado de hacer explícita las propiedades lógicas de una proposición del lenguaje natural mediante su formalización. Esto es, una forma lógica puede explicitarse al considerar el resultado de simbolizar nuestras proposiciones del lenguaje natural a partir de expresiones del lenguaje lógico disponible.

Forma del concepto

Es la figuración que posee un cuerpo en su exteriorización, así reconocemos formas rectangulares, cuadradas, redondas, rectangulares, etcétera, y distintas formas en un mismo cuerpo.

Aristóteles distinguió entre sustancias primeras, que son los individuos que componen una especie, y éstas a su vez un género. Éstas, especie y género, son las sustancias segundas con idea de universalidad. Ejemplo de sustancias primeras, serían Buenos, Aires, Lima, Montevideo, y de sustancias segundas, las ciudades, sustancias más abarcativas y universales. Las sustancias primeras están compuestas por materia y forma, por un lado y potencia y acto, por otro. Tomando el primer par de elementos, daremos un ejemplo de sustancia primera: la mesa del comedor de mi casa (una mesa concreta). En ella se reúnen una materia, la madera, y una forma que hace que eso sea una mesa y no por ejemplo, una silla. O sea, que para Aristóteles la forma es la que hace que la sustancia primera sea eso, y no otra cosa. La forma es determinante de la materia. Ésta se comporta de modo pasivo, mientras lo activo es la forma, que le imprime su especial individualidad a la materia. Ambos términos, materia y forma son inseparables, ya que no puede existir una sin la otra. La forma separada de la materia, solo existe en el pensamiento, como idea. Puede ser que existan cosas cuadradas, redondas, o rectangulares de distintas materias, pero siempre tendrán alguna. Podemos concluir que forma es la esencia de las cosas, porque hace que sean eso y no otra cosa.

Pitagoras (582 a. C-507 a. C) consideró que la forma de las cosas, que las diferenciaba de otras, era el número. Immananuel Kant (1724-1804), expresó su pensamiento de que el conocimiento se inicia en el mundo sensible, pero a esta materia hay que darle forma, para ordenar la experiencia caótica y crear el fenómeno. Las formas puras, dadas a priori a la materia son el espacio y la forma. Será la razón la que ordene la materia informe, mediante las categorías que se presenta a los sentidos. Materia y forma solo son susceptibles de dividirse, solo en forma abstracta.

Aplicaciones específicas del concepto de forma:

Se habla de forma refiriéndonos a la estructura, por ejemplo de un poema o de una obra musical, o a un género musical particular.

También se emplea el término para referirnos a un físico bien moldeado, para decir: ¡Qué buenas formas!

Otro uso del vocablo es para hablar de formas de gobierno, para indicar los distintos modos en que los estados ejercen su poder. Las formas de estado hace referencia a como organizan los estados ese poder, espacialmente.

Hemos escuchado también la expresión: “Su forma de hablar es grosera” manifestando que su modo de dirigirse hacia los demás no es el correcto según no solo la estructura del lenguaje, sino al contenido utilizado en el vocabulario.

 Forma de juicio

El juicio es la forma de pensar, mediante la cual el hombre refleja la conexión objetiva de los lados, propiedades y momentos singulares en los objetos y fenómenos. Los juicios se expresan en el lenguaje en forma de proposiciones (“La rosa es roja”). En los juicios más simples se refleja la dialéctica objetiva que es inherente a la Naturaleza. “Comenzando por lo más simple, lo más corriente, lo más popular”, &c., por una proposición CUALQUIERA: “las hojas del árbol son verdes”; “Juan es un hombre”; “Boby es un perro”; &c., hay ya en ello (como genialmente lo hizo notar Hegel) dialéctica: lo que es SINGULAR es general” (Lenin). La forma más simple de juicio es la que registra un hecho singular, por ejemplo, “el frotamiento produce calor”. El desarrollo del conocimiento conduce a un grado más alto de juicios, por ejemplo, “todo movimiento mecánico puede, con la ayuda del frotamiento, convertirse en calor”. El ulterior desarrollo de la ciencia conduce a la universalidad, al descubrimiento de la ley universal de la Naturaleza: “cualquier forma de movimiento puede y debe convertirse en cualquier otra forma de movimiento”. La existencia de diversas formas de juicio, está condicionada por el desarrollo histórico del conocimiento sobre la base de la práctica material social. Por eso, las formas de juicio no pueden ser explicadas y comprendidas como formas puras, es decir, al margen del contenido real del conocimiento, al margen de la historia de las diversas ciencias. Esto no lo puede comprender la lógica formal, que concibe el juicio como la mera forma de pensar.

 El juicio es definido por la lógica formal como la conexión de nociones o de representaciones. El criterio fundamental de la veracidad de los juicios en la lógica formal, es el principio de la incompatibilidad de los juicios contradictorios entre sí. La lógica formal enseña que de dos juicios contradictorios, siendo uno de ellos verdadero, el otro resulta forzosamente falso; con la falsedad de uno de ellos, el otro resulta verdadero. Por ejemplo, de los dos juicios: “Juan es bueno” y “Juan no es bueno”, siendo verdadero el primero, el otro debe ser forzosamente falso, y con la falsedad de uno, verdadero el otro. No obstante la evidencia aparente de esta ley, ella no sirve para determinar la veracidad o falsedad del juicio. La lógica dialéctica enseña a diferenciar estrictamente los juicios verdaderos de los juicios falsos, pero el criterio lógico-formal para tal diferenciación es absolutamente insuficiente, puesto que no se refiere al contenido del juicio. Por ejemplo, el juicio: “la materia es continua y discontinua”, según la lógica formal, debe ser reconocido como falso, pro en realidad, este juicio, como lo está probando la ciencia contemporánea, refleja con profunda justeza la esencia de la materia. El único criterio de la verdad de los juicios es su consonancia con la realidad objetiva.

Forma del Razonamiento:

El razonamiento es el proceso intelectual y lógico del pensamiento humano. El razonamiento entrega argumentos sobre las conexiones mentales incurridas que justifican un determinado pensamiento.

La palabra razonamiento viene del latín ratio que significa razón junto con el sufijo-iento que indica el resultado de algo.

En filosofía, el razonamiento está íntimamente ligado a la lógica. El razonamiento usa la lógica para crear un proceso intelectual con las premisas o datos ya conocidos y comprobados para deducir o inferir datos que no son conocidos con el fin de llegar a una conclusión. A esto se le llama razonamiento lógico.

El razonamiento por lo tanto es la inferencia o deducción de información a través de premisas para llegar a una conclusión. Existen varios tipos de razonamientos como el razonamiento deductivo y el inductivo.    

                                                                                         

1.4 Definición del Concepto de Conocimiento Inferido

Se obtiene a través de verdades preestablecida, aplicando las leyes de la lógica a proposiciones verdaderas, es decir que al momento de resolver un problema práctico nos vemos obligados a menudo a apoyarnos no en la experiencia inmediata, sino en el saber anteriormente adquirido.

Ej. Sobre las Distintas enfermedades que está expuesto el hombre, esto ha hecho a que Evolucione constantemente la Medicina Gracias a las experiencias que han sido todo un éxito en el pasado, esto ha hecho a encontrar una infinidad de curas contra distintas enfermedades que en su tiempo eran mortales.

2. EL JUICIO COMO CÉLULA FUNDAMENTAL DEL PENSAMIENTO

La lógica formal, analiza el juicio en tanto en cuanta premisa del razonamiento, es decir en relación tan solo  con la doctrina de la estructura de las demostraciones.

La esencia de la doctrina de Aristóteles sobre el juicio es la siguiente

La verdad o el error existen solo si hay afirmación  o negación.

La afirmación o negocio de algo  equivale a un juicio.

Solo con referencia al juicio, cabe plantear el problema de la verdad o falsedad

No significa algo, pero no son ni verdaderos ni erróneos  y por ello no contiene ningún juicio.

El juicio es verídico, si en el aparece unido, lo que está unido en la realidad y separado, lo que en ella está separado.

El juicio es falso si en el está unido lo que en la realidad está separado y separado lo que en ella figura unido.

Los lógicos idealistas, niegan el contenido objetivo del pensamiento, consideran el juicio como forma pura, totalmente indiferente a todo contenido y no solo al concreto, formulan concepto de la ¨función prepositiva ¨ que según ellos es una expresión que contiene uno o varias  variables, esta se convierte en juicio cuando las variables se sustituyen por constantes.

Según Rossell; las funciones del juicio pueden ser de tres clases: Verídicas con todos los significados del argumento o argumentos.

Falsas con todos los significados.

Verídicos con unos argumentos y falsas con otros.

Desde el punto de vista de la forma, el juicio se caracteriza por la estructura de  sujeto y predicado  que es general para todos los juicios y las proposiciones de tres términos, gracias a ello comprendemos la misma facilidad del pensamiento que el hombre de la antigüedad ha dejado en los monumentos.

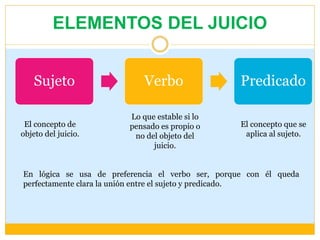
Todo juicio tiene tres elementos:

a) Un concepto sujeto.

b) Un concepto predicado.

c) Una cópula. La forma lingüística de un juicio es la “proposición”

Clasificación de los Juicios:

Siguiendo la clasificación kantiana de los juicios, encontramos que pueden dividirse por su cantidad, por su cualidad, por la relación de la cópula y por su modalidad.

Los juicios, según su cantidad, pueden ser:

a) Universales, si toman al sujeto en toda su extensión;

b) Singulares, si el sujeto es un concepto individual y, como tal, toma al sujeto individual en toda su extensión.

Por eso, podemos incluir los juicios individuales entre los universales. Los juicios, según su cualidad o calidad, pueden ser:

a) Afirmativos, si el sujeto está incluido en el predicado;

b) Negativos, si el sujeto no está incluido en el predicado;

c) Indefinidos, si la inclusión no es clara porque niega la posibilidad de que el sujeto esté incluido fuera del predicado.

Este juicio puede llevar a la formulación de un juicio afirmativo.  Según la relación de la cópula, los juicios pueden ser:

a) Categóricos, si se refieren a la sustancia del concepto sujeto. No expresan limitaciones en la relación entre sujeto y predicado.

b) Hipotéticos, si se refieren a la relación de causa entre sujeto y predicado. Establecen una condición para que se de la relación.

c) Disyuntivos, si se refieren a la acción recíproca entre dos o más predicados.

Proponen una alternativa para que se dé la relación.  Según su modalidad, los juicios pueden ser:

a) Problemáticos, si expresan una posibilidad.

b) Asertóricos, si expresan una realidad del hecho.

c) Apodícticos, si expresan una relación necesaria.

De entre los juicios anteriores, nos interesan especialmente los “juicios categóricos”, pues son los que servirán para construir las relaciones fundamentales de los razonamientos.

Como sabemos que el juicio en sí no es observable, por suceder dentro de la mente, deberemos limitarnos al estudio de sus expresiones lingüísticas, es decir, de sus proposiciones. Por eso es que hablamos de “proposiciones categóricas”. Si observamos las variaciones posibles en la cantidad y en la cualidad de las proposiciones categóricas, encontraremos que existen cuatro tipos, a los que Copi llama “formas típicas” de las proposiciones categóricas. Cada una de estas formas típicas está simbolizada por una letra vocal mayúscula, tomada de las palabras latinas “affirmo” y “nego”, de la siguiente manera:

a) Universal y afirmativa               A

b) Universal y negativa                 E

c) Particular y afirmativa                I

d) Particular y negativa                 O

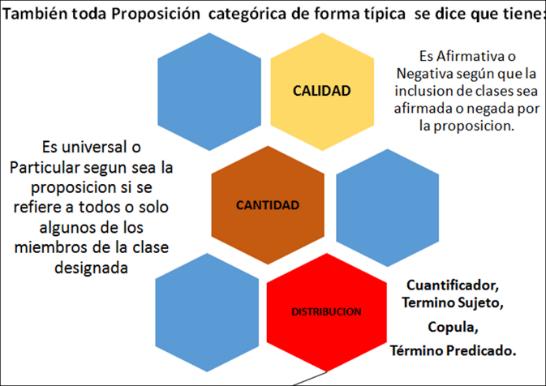
Toda proposición categórica de forma típica empieza por un “cuantificador”, es decir, una partícula que expresa cantidad (todo, algún, ningún); un “término sujeto”, que expresa un concepto sujeto; luego la “cópula”, que en el caso de la particular negativa va precedida de un “negador”; y un “término predicado”, que expresa un concepto predicado.

1.2 Proposiciones categóricas

Las proposiciones categóricas son aquéllas que hacen afirmaciones incondicionales. Por ejemplo, “todos los hombres son mortales” es una proposición categórica, mientras que “si tengo el día libre, voy a la playa” no lo es, ya que hay un condicionante para el hecho de ir a la playa: que tenga el día libre. La forma general de toda proposición categórica es la siguiente: cuantificador + sujeto + cópula + predicado Donde:

• El cuantificador determina si la proposición se refiere a todos los sujetos de un conjunto, a una parte de ellos o sólo a un elemento del conjunto.

• El sujeto es el conjunto o subconjunto de individuos o cosas de los que trata la proposición.

• La cópula (es decir, lazo) es el verbo que une al sujeto con el predicado. Tiene la doble función de llevar a cabo esta relación y de hacer posible el enunciado.

1.3 Calidad, Cantidad y Distribución de las proposiciones categóricas.

Las proposiciones categóricas, en cuanto a calidad, puede ser afirmativas o negativas. Son afirmativas cuando el predicado asigna al sujeto alguna característica o cualidad, por ejemplo: es estudiante, son voladoras. Son negativas cuando el predicado niega al sujeto la característica o cualidad, por ejemplo: no es estudiante, no son voladoras.

En cuanto a cantidad, las proposiciones categóricas pueden ser universales, particulares o singulares. Son universales cuando se refieren a la totalidad del conjunto de los sujetos. Son particulares cuando se refieren sólo a una parte del conjunto de los sujetos y son singulares cuando se refieren a sólo un miembro específico del conjunto de los sujetos.

De la combinación de estas cuatro categorías se obtiene lo que se conoce como las cuatro formas clásicas de las proposiciones categóricas:

a) Universal afirmativa, o tipo A.

b) Particular afirmativa, o tipo I.

c) Universal negativa, o tipo E.

d) Particular negativa, o tipo O.

Los nombres de las categorías A e I han sido tomadas del vocablo latino AFFIRMO, que significa afirmo. Estas vocales designan a las proposiciones afirmativas universales y afirmativas particulares, respectivamente. E y O, en cambio, han sido tomadas del vocablo latino NEGO, que significa niego. Estas vocales designan a
las proposiciones negativas universales y negativas particulares, respectivamente. Las proposiciones universales afirmativas.

Las proposiciones tipo A tienen la siguiente forma:

Todo S es P.

Donde S se refiere al conjunto o clase sujetos y P se refiere al predicado o a la clase predicados.

La denominación universal afirmativa es apropiada, porque la proposición afirma que hay una relación de inclusión entre las dos clases y, además, que la inclusión es completa o universal, es decir, que todos los miembros de S son también miembros de P.

Las proposiciones particulares afirmativas:

Las proposiciones tipo I tienen la siguiente forma:

Algún S es P.

Esta proposición se interpreta afirmando que al menos un miembro de la clase designada por S es también un miembro de la clase designada por P. Su denominación es apropiada porque la proposición afirma la presencia de una relación de inclusión entre las clases, pero no lo afirma de la primera clase universalmente, sino sólo parcialmente, únicamente de algunos miembros de la primera clase, de por lo menos un miembro de la clase S.

Las proposiciones universales negativas

Las proposiciones tipo E son aquellas que siguen la forma:

Ningún S es P.

El nombre universal negativa es apropiado porque la proposición niega que haya una relación de inclusión entre las dos clases y lo niega universalmente, ya que ninguno de los miembros de S es miembro de P, y viceversa.

Las proposiciones particulares negativas

Las proposiciones categóricas tipo O siguen la forma:

Algún S no es P.

Este tipo de proposiciones afirma que al menos un miembro de la clase designada por el término S está excluido de la clase designada por el término P.

Proposiciones singulares

Las proposiciones categóricas particulares son aquellas que se refieren a un sujeto específico o singular. Estas proposiciones se tratan igual que las universales, dado que relacionan al único elemento de S con la clase P. Por ejemplo:

•Juan es estudiante, es una proposición singular afirmativa.

•Luis no es nadador, es una proposición singular negativa.

 Ejemplos de proposiciones categóricas.

A continuación, veremos varios ejemplos de proposiciones y las clasificaremos de acuerdo a las categorías A, I, E y O, recién comentadas.

Ejemplo:

Se trata de la proposición:

Los políticos mienten por costumbre.

Esta proposición es de tipo verbal, pero puede transformarse en la siguiente proposición nominal:

Los políticos son mentirosos.

Que se entiende como una proposición universal de tipo A:

Todos los políticos son mentirosos.

Las proposiciones categóricas pueden diferir entre sí en la calidad, cantidad o en ambas, y con base en éstas diferencias se han construido un conjunto de inferencias inmediatas.

Los lógicos de otros tiempos dieron a este género de inferencias inmediatas el nombre de “oposición” y establecieron importantes relaciones entre los valores de verdad de los juicios que difieren en los aspectos mencionados.

Las proposiciones que difieren tanto en cantidad como en calidad se dice que son contradictorias. Las proposiciones universales que difieren sólo en calidad se dice que son contrarias. Las particulares que difieren en calidad son subcontrarias. Las que difieren en cantidad, pero no en calidad, están en relación de subalternación.

Reglas de oposición.

Ley de Contradictorias.- Dos proposiciones con un mismo sujeto y predicado, y que difieren tanto en la calidad como en la cantidad, son contradictorias; es decir, definen la relación de A con respecto de O, y de E con respecto de I, y viceversa. Ésta es la oposición mostrada con las líneas diagonales.

La Ley de Contradictorias establece que dos proposiciones contradictorias no pueden ser al mismo tiempo ni Falsas ni Verdaderas.

Ley de Contrarias.- Dos proposiciones son contrarias si son proposiciones universales que teniendo el mismo sujeto y el mismo predicado difieren en calidad; es decir, A respecto de E y viceversa. Ésta es la oposición mostrada por la línea horizontal superior.

La Ley de las Contrarias establece que dos proposiciones contrarias no pueden ser ambas verdaderas, pero pueden ser ambas falsas.

Ley de Subcontrarias.- Dos proposiciones son contrarias si son proposiciones particulares que teniendo el mismo sujeto y el mismo predicado difieren en calidad; es decir, I respecto de O y viceversa. Ésta es la oposición mostrada por la línea horizontal inferior.

La Ley de las Subcontrarias establece que dos proposiciones subcontrarias no pueden ser ambas falsas, pero pueden ser ambas verdaderas.

Ley de Subalternancia.- Son proposiciones subalternas aquéllas que teniendo el mismo sujeto y el mismo predicado, sólo difieren en cantidad y no en calidad, es decir, A con respecto a I, y E con respecto a O. La proposición universal se llama subalternante, la particular correspondiente se denomina subalterna.

La Ley de Subalternancia establece que de la verdad de la subalternante se infiere la verdad de la subalterna, pero de la falsedad de aquella no hay inferencia válida con respecto a ésta.

 

2.2 Simbolización y diagramas de las proposiciones típicas

Categoría Forma

Universal afirmativa, tipo A Todo S es P.

Particular afirmativa, tipo I Algún S es P.

Universal negativa, tipo E Ningún S es P.

Particular negativa, tipo O Algún S no es P.

Las leyes de oposición describen las relaciones entre estas categorías y nos permiten realizar inferencias inmediatas. Calidad, cantidad y distribución.

Proposiciones Categóricas de Forma Atípica

Las formas un poco rígidas A, E, I y O, no son las únicas en las que pueden expresarse las proposiciones categóricas.

Muchos silogismos categóricos contienen proposiciones en forma no típica. Para reducir estos razonamientos a forma típica es necesario traducir sus proposiciones componentes a forma típica. Describiremos ahora algunos de los métodos para traducir proposiciones de forma no típica a forma típica.

Debemos mencionar en primer término las proposiciones singulares, tales como "Sócrates es un hombre" y "Esta mesa no es una antigüedad". Estas proposiciones no afirman ni niegan la inclusión de una clase en otra, sino que afirman o niegan que un individuo o un objeto determinados pertenezcan a una cierta clase. Se acostumbra considerar las proposiciones", singulares como si ya estuvieran en forma típica, tratando las afirmativas como las universales afirmativas y las negativas como las universales negativas. El primer grupo de proposiciones categóricas que requieren traducción a forma típica es' el formado por las proposiciones que, en lugar de sustantivos o términos de clase, tienen adjetivos o frases adjetivales como predicados. Por ejemplo, " Algunas flores son hermosas" y "No hay ningún barco disponible para el servicio activo" se apartan de la forma típica, solamente en que sus predicados "hermosas" y "disponible pará servicio activo" se refieren a propiedades, en vez de referirse a clases.

Pero toda propiedad determina una clase, la clase de todas las cosas que tienen esa propiedad; así, a toda proposición de ese tipo le corresponde una proposición lógicamente equivalente que adopta la forma típica. A los dos ejemplos citados, ‘corresponden las preposiciones I y E Algunas flores son bellezas y no hay ningún barco de guerra que sea, una cosa disponible para el servicio activo, Si una proposición categórica está en forma típica, pero tiene un predicado adjetival en vez de un término de predicado, se puede hacer la traducción a forma típica remplazando el predicado adjetival por un término que designe la clase de todos los objetos de los cuales tal adjetivo puede predicarse verazmente.

Debemos considerar ahora las formulaciones de proposiciones categóricas en las cuales los verbos principales son distintos de la cópula de la forma típica ser. Ejemplos de este tipo son "Todos los hombres anhelan el reconocimiento de sus semejantes" y "Algunos hombres beben". El método común para traducir tales enunciados a la forma típica es considerar que, exceptuando el término sujeto y el cuantificador, designan una característica definitoria de una clase; luego se remplaza el verbo por una cópula típica y el predicado por un término que designe a la clase determinada por la mencionada característica definitoria de la clase. Así, los dos ejemplos citados se traducen a la forma típica por las siguientes proposiciones categóricas: Todos los hombres son seres deseosos de alcanzar el reconocimiento de sus semejantes y Algunos hombres son bebedores.

Otro tipo de enunciado que es fácil verter a la forma típica es aquel en el cual están todos los ingredientes de la forma típica, solo que no están ordenados de la manera propia de ésta. Dos ejemplos de este tipo son: "Los caballos de carrera son todos de pura raza" y "todo está bien si termina bien".

En tales casos debemos decidir cuál es el término sujeto y luego ordenar las palabras de modo que expresen una proposición categórica de forma típica. Es obvio que los dos enunciados precedentes pueden verterse en las proposiciones A Todos los caballos de carrera son de pura raza y Todas las cosas que terminan bien son cosas que están bien.

Las cantidades de muchas proposiciones categóricas no se hallan indicadas por los cuantificadores de forma típica ‘todos’, 'ningún' y 'algunos'. Los enunciados que contienen las palabras 'cada' y 'cualquier' pueden traducirse fácilmente.

Las proposiciones 'A cada chancho le llega su San Martín' y 'Cualquier contribución será bien recibida' se puede traducir:

Todos los chanchos son seres a los que les llega su San Martín, y Todas las contribuciones son cosas que se reciben bien. Similares a 'cada' y 'cualquier' son 'cada cosa' y 'cualquier cosa', y paralelas a éstas, pero claramente 'restringidas a clases de personas, son 'cada uno', 'cualquiera', 'quienquiera', 'quien', 'aquel que', etc. Estas palabras no pueden originar ninguna dificultad. También los artículos gramaticales 'un' y 'el' pueden servir para indicar cantidad. El primero, en algunos contextos significa todos y en otros significa algunos. Así, "Un murciélago no es un ave" y "Un elefante es un paquidermo" deber; interpretarse como Todos los murciélagos son no-aves ( o ningún murciélago es un ave) y Todos los elefantes son paquidermos. Pero, "Un murciélago entró por la ventana" y "Escapó un elefante" obviamente no se refieren a todos los murciélagos o a todos los elefantes; su traducción más adecuada sería Algunos murciélagos son seres que entraron por la ventana y Algunos elefantes son seres que escaparon.

La palabra 'el' (o 'la', o 'los', o 'las') puede usarse para referirse a un individuo particular o a, todos los miembros de una clase. Pero, en este caso hay muy poco o ningún riesgo de caer en la ambigüedad. Pues un enunciado como "La ballena es un mamífero" se traduce en casi todos los contextos como la proposición A Todas las ballenas son mamíferos, mientras que la proposición singular El primer presidente fue un héroe militar se halla ya en forma típica como proposición A. Las proposiciones categóricas que contienen las palabras 'solamente' o 'nadie más que' suelen llamarse proposiciones 'exclusivas', porque en general afirman que el predicado se aplica exclusivamente al sujeto nombrado. Son ejemplos de tales proposiciones: "Solamente los ciudadanos pueden votar" y "Nadie más que los valientes merecen la doncella", que son traducibles a las proposiciones categóricas de forma típica: Todos los que pueden votar son ciudadanos y Todos los que merecen la doncella son aquellos que son valientes. Las llamadas proposiciones exclusivas, que comienzan con 'solamente' o 'nadie más que', son traducibles a proposiciones A cuyos términos sujeto y predicado son los términos predicado y sujeto, respectivamente, de la proposición exclusiva. Hay contextos en los cuales 'Solamente S es P' o 'Nadie más que S es P' quieren significar, no simplemente que Todo p es S, sino también que Todo S es p o que Algún S es Po Sin embargo, no siempre ocurre así. Allí donde el contexto contribuye a determinar el significado, debe tomárselo en consideración, naturalmente; pero, en la ausencia de tal información adicional, las traducciones apropiadas son las que hemos indicado.

Algunas proposiciones categóricas no contienen palabras para indicar la cantidad, por ejemplo, "Se prohíbe entrar con, perros" y "Hay niños presentes". Donde no hay cuantificadores puede ser dudoso lo que el enunciado pretende expresar y solo podemos determinar su significado -examinando el contexto en el cual aparece. Sin embargo, los dos ejemplos citados son bastante claros. El primero probablemente se refiere a todos los perros, mientras que el segundo es más probable que se refiera solamente a algunos niños. Sus traducciones a forma típica son: Todo S los perros son seres con los que no se puede entrar y Algunos niños son seres que están presentes.

Debemos examinar ahora brevemente algunas proposiciones que no se asemejan para nada a las proposiciones categóricas de forma típica, pero que pueden ser traducidas a ellas.

Ejemplos de ellas son: "No todos los niños creen en Papá Noel", "Hay elefantes blancos", '"No hay elefantes rosados" y Nada puede ser al mismo tiempo redondo y cuadrado". Si reflexionamos un momento sobre estas proposiciones, concluiremos que se las puede traducir a las siguientes proposiciones de forma típica, a las cuales son lógicamente equivalentes:

Algunos niños no son creyentes en Papá Noel, Algunos elefantes son blancos, Ningún elefante es rosado y Ningún objeto redondo es también un objeto cuadrado.

Debemos observar que muchas proposiciones indican la cantidad de manera más explícita de lo que lo hacen las proposiciones de forma típica. Se realiza la especificación mediante el uso de cuantificadores numéricos o casi-numéricos, tales como 'uno', 'dos', 'tres', 'muchos', 'pocos', 'la mayoría " 'casi todos', etc. Pero los razonamientos cuya validez depende de datos numéricos o casi-numéricos .son silogísticos, y exigen un análisis más penetrante que el suministrado por la teoría simple del silogismo categórico. Todo silogismo categórico que contenga proposiciones numéricas o casi-numéricas de este tipo, no altera su validez o su invalidez cuando se traducen esas proposiciones a forma típica de manera tal que sus aspectos numéricos o casi-numéricos simplemente se dejan de lado. Así, para todos los propósitos relacionados con el silogismo categórico, podemos traducir "Había un estudiante en el baile", "Había dos estudiantes en el baile", etc., y "Había pocos estudiantes en el baile", "Había muchos estudiantes en el baile" y "La mayoría de los estudiantes estaban en el baile" indistintamente como: Algunos estudiantes son personas que estaban en el baile; Sin embargo, algunos cuantificadores casi-numéricos no pueden traducirse de manera tan simple, entre otros: 'casi todos', 'no todos', 'todos excepto unos pocos'. 'casi cada uno'.

Las proposiciones en las cuales aparecen estas expresiones como cuantificadores son proposiciones 'exceptivas', que hacen dos afirmaciones en vez de una. Son del mismo tipo que las proposiciones explícitamente exceptivas, tales como: “Todos son elegibles excepto los empleados", "Menos los empleados, todos son elegibles" y "Solamente los empleados no son elegibles", Cada una de estas proposiciones lógicamente equivalentes afirma, no solamente que Todos no son elegibles, sino también que Ningún empleado es elegible. Si ponemos 'S' en lugar de 'empleados' y 'P' en lugar de 'personas elegibles', podemos escribir estas dos proposiciones así: Todo no-S es p y Ningún. S es P. Es indudable que estas proposiciones son independientes y conjuntamente afirman que las clases S y p son complementarias.

Cada una de estas proposiciones exceptivas es compuest
a y, por tanto, no pueden ser traducidas a una proposición categórica de forma típica simple, sino más bien a una conjunción explícita de dos proposiciones categóricas de forma típica.

Así, las tres proposiciones acerca de la elegibilidad se traducen idénticamente a: Todos los no- empleados son personas elegibles y Ningún empleado es una persona elegible. Las siguientes proposiciones exceptivas con cuantificadores casi-numéricos son, también, compuestas: "Casi todos los estudiantes estaban en el baile", "No todos los estudiantes estaban en el baile". "Excepto unos pocos, todos los estudiantes estaban en el baile", "Solamente algunos estudiantes estaban en el baile".

Cada una de estas proposiciones afirma que algunos - estudiantes estaban en el baile y niega que Todos los estudiantes estuvieran en el baile. La información casi-numérica que presentan carece de importancia desde el punto de vista de la inferencia si logística y se traducen todas indistintamente como Algunos estudiantes son, personas que estaban en el baile y Algunos estudiantes no son personas que estaban en el baile.

Las proposiciones exceptivas pueden aparecer, y efectivamente aparecen, en razonamientos silogísticos del lenguaje ordinario. ¿Cómo se puede determinar la validez o invalidez de un silogismo categórico que contiene una proposición exceptiva? Ello depende de la posición que tenga dentro del razonamiento la proposición exceptiva. Si es una premisa, entonces puede someterse el razonamiento a dos pruebas separadas.

Consideremos, por ejemplo, el siguiente razonamiento: "Todos los que vieron el partido estuvieron en el baile; no todos los estudiantes estuvieron en el baile; luego, algunos estudiantes no vieron el partirlo", Su primera premisa y su conclusión son proposiciones categóricas que pueden traducirse fácilmente a forma típica. Pero su segunda premisa, por ser una proposición exceptiva, no es simple sino compuesta. Para saber si las premisas implican o no la conclusión, primeramente debemos someter los métodos de prueba al silogismo formado por la primera premisa del razonamiento dado, la primera mitad de su segunda premisa y su conclusión. Reducidas las proposiciones a la forma típica, tenemos:

Todas la" personas que vieron el partido son personas que estuvieron en el baile. Algunos estudiantes son personas que estuvieron en el baile.

Por tanto, algunos estudiantes no son personas que vieron el partido.

Este silogismo categórico de forma típica es de la forma AIO-2 y viola la regla 2, ya que incurre en la falacia del Término medio no distribuido. Pero aún no se ha demostrado que el razonamiento original no sea válido, pues el silogismo examinado sólo contiene parte de las premisas del razonamiento original. Debemos ahora analizar el silogismo formado por la primera premisa y la conclusión del razonamiento original, juntamente con la segunda mitad. de la segunda premisa. Reducido todo a forma típica, tenernos:

Todas las personas que vieron el partido son personas que estuvieron en el baile. Algunos estudiantes no son personas que estuvieron en el baile.

Por tanto, algunos estudiantes no son personas que vieron el partido. Este silogismo categórico de forma típica es de forma diferente, A00-2, y se ve fácilmente que es válido. Por consiguiente, el razonamiento original es válido, pues la conclusión es la misma y las premisas del razonamiento original incluyen las premisas de este silogismo de forma típica válido. Así pues, para determinar si es o no válido un silogismo de forma no-típica, una de cuyas premisas es una proposición exceptiva, puede ser necesario someter a una prueba de validez a dos silogismos categóricos de forma típica diferentes. Si las premisas de un razonamiento son ambas proposiciones categóricas y su conclusión es una proposición exceptiva, sabemos que no es válido, pues aunque las dos premisas categóricas puedan implicar una u otra mitad de la conclusión compuesta, no pueden implicarlas a ambas. Finalmente, si un razonamiento contiene proposiciones exceptivas como premisas y como conclusión, para saber si es o no válido puede ser necesario someter a prueba todos los silogismos que se puedan construir sobre la base del razonamiento original. Las explicaciones dadas bastan para permitir al estudiante resolver con éxito tales problemas.

Es importante adquirir cierta facilidad para traducir proposiciones de forma no-típica a forma típica, pues los métodos que hemos expuesto para determinar si un silogismo es O no válido, solo pueden aplicarse a silogismos categóricos de forma típica.